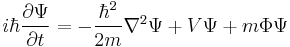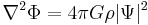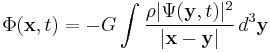Schrödinger–Newton equations
The Schrödinger–Newton equations are modifications of the Schrödinger equation and derived from Gauss' law for gravity, proposed by Roger Penrose in The Road to Reality, that mathematically describe the basis states involved in a gravitationally-induced wavefunction collapse scheme:
where 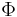 is a quasi-Newtonian potential given by
is a quasi-Newtonian potential given by
and  is the classical mass density. It can be shown that these equations conserve probability, momentum etc., as the Schrödinger equation does.
is the classical mass density. It can be shown that these equations conserve probability, momentum etc., as the Schrödinger equation does.
Their Lie point symmetries are rotations, translations, scalings, a phase change in time, and a Galilean transformation of sorts that looks like the equivalence principle at work.